Topographic effects on different types of baroclinic instability
In Lobo et al. (2025), we study how the consideration of an interior potential vorticity gradient alters the effects of sloping bottom topography on baroclinic instability.
Here are a couple of animations of potential vorticity evolution, made using a modified version of GeophysicalFlows.jl, that demonstrate the varying effects of topography on different types of instability. Importantly, we use a three-layer model, allowing for the representation of an interior potential vorticity gradient. We also use the power iteration method (see Paloczy and LaCasce (2022)) to simulate a growing mode and perform an empirical linear stability analysis, of sorts. Thus, the animations below are of a growing, unstable wave.
The main takeaway is that studies that use two-layer models to simulate topographic effects on baroclinic instability only show part of the picture. Representing this modal instability with two layers will surely affect the instability since the instability must always exist in both layers! Allowing for a surface-intensified mode to form in the upper two layers of a three-layer mitigates topographic effects on the instability.
The first animation shows how a surface-intensified Charney-type unstable wave is fairly apathetic of bottom topography, though there are still implications for how energy is transferred down and dissipated through bottom drag.
In this second animation we look at how topography affects the growing, unstable mode of a full-column Eady-type mode. Positive sloping topography (middle) slows down the growth rate of the instability but doesn’t change the unstable wavenumber, whereas negatively sloping topography (right) moves the instability to a higher wavenumber. These results more closely correspond to studies that have used a two-layer model to study topographic effects on baroclinic instability.
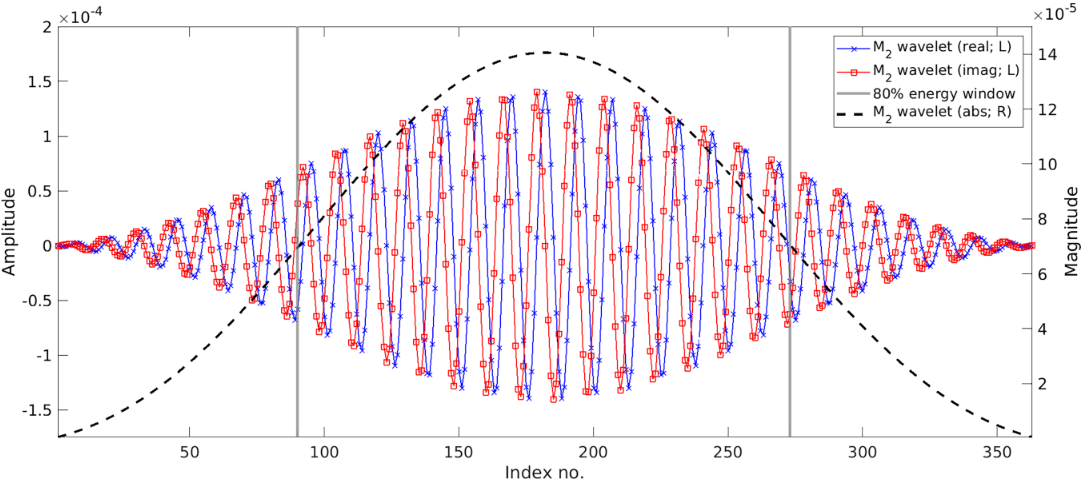
CWT_Multi: Wavelet analysis of nonstationary tides
I am the lead author of a recent study where we develop a math method for analyzing nonstationary tidal signals that quickly evolve in time. The CWT_Multi code is available on Github. In the CWT_Multi documentation, I provide a comprehensive and readable primer on the math theory of CWT_Multi, as well as some example code. The details of the method and its application can be found in Lobo et al., (2024).
CWT_Multi can be used to analyze the time evolution of nonstationary tidal amplitudes and phases in response to external factors, e.g., estuarine flooding. In addition, CWT_Multi reconstructs a time series from the nonstationary tidal amplitude data. The tide-only time series could, for example, then be subtracted from the original signal to study phenomena unrelated to tides, e.g., storm surge due to rainfall.
DIY rotating tank
I recently scrapped together a rotating tank setup (with a phone mount) from an old record player and some nuts and bolts. The video below shows some eddies forming in the tank as viewed from a non-inertial, rotating frame of reference.
In the future I plan on using the tank to exhibit topographic Rossby waves and baroclinic instability.

Shallow water tide model with self-attraction and loading
I made a linear, single-layer, viscous, non-rotating shallow water model with tidal and wind forcing to explore using different predictor and predictor-corrector schemes when applying self-attraction and loading (SAL) forcing in an ocean model.
